효율적인 추론을 위한 벡터 양자화 베이지안 딥러닝

TL; DR

• 베이지안 딥러닝은 전통적인 딥러닝이 겪는 다양한 문제를 극복하는 유망한 방법입니다. 하지만, 베이지안 딥러닝은 하나의 데이터에 대한 결과를 유도하기 위해 수십 번의 추론을 요구합니다. 따라서, 베이지안 딥러닝은 전통적인 딥러닝에 비해 결과 예측하는데 걸리는 시간이 수십 배 증가한다는 문제가 있습니다.
• 이 문제를 극복하기 위해, 우리는 벡터 양자화 베이지안 뉴럴 네트워크를 제안합니다. 이 방법은 데이터에 대해 한 번만 추론을 수행하며, 이를 사전에 미리 기억된 예측으로 보완합니다.

베이지안 딥러닝은 불확실성을 추론할 수 있으며 데이터 손상에 강건합니다

딥러닝은 다양한 분야에서 매우 높은 성능을 성취했습니다. 하지만, 이제까지 딥러닝이 해결하지 못한 다음과 같은 두 가지 중요한 문제가 있습니다.

1. 불확실성의 추론(uncertainty estimation): 딥러닝은 신뢰할 수 있는 확률을 추론하지 못합니다. 예를 들어, 분류 문제에서 우리는 딥러닝 결과의 Softmax 값을 확률로 해석하고는 합니다. 하지만, 이것은 우리가 기대하는 ‘추론 결과가 정답을 맞출 확률’과는 상당한 차이가 있습니다. 실제로는 Softmax로 유도된 정답에 대한 신뢰도(Max(Softmax(nn_logit)))는 실제 정답을 맞출 확률에 비해 높은 값을 가집니다. 이를 ‘딥러닝은 결과를 과신(overconfident)하는 경향이 있다’고 합니다.

2. 손상된 데이터에 대한 강건성(rubustness): 딥러닝은 입력에 작은 노이즈를 더함으로써 완전히 잘못된 결과를 유도하게 하는, 적대적 공격(adversarial attack)에 취약한 경향을 보입니다. 또한, 날씨의 변화나 모션 블러(motion blur), 초점 흐림(defocus)와 같은 자연적으로 손상된(corrupted) 이미지의 분류 정확도가 심각한 수준으로 훼손됩니다. 심지어, 딥러닝의 입력값을 수 픽셀 수평이동하는것만으로 결과값이 교란되기도 합니다.

뉴럴넷 판단은 항상 틀릴 수 있으며, 위와 같은 딥러닝의 특성은 안정성이 특히 중요한 응용 분야에 치명적인 결과를 초래할 수도 있습니다. 이를테면, 자율주행 기능이 탑재된 차량이 차 앞에 다른 차량이 있음에도 아무것도 없다고 잘못 판단한다면 추돌사고가 일어날 수 있을 것입니다. 하지만, 자율주행 시스템이 판단이 잘못됐을 확률까지 동시에 추론한다면 보다 방어적으로 시스템을 운용할 수 있을 것입니다. 더불어, 야간이나 안개까 낀 상황에도 자율주행 시스템은 안전하게 차량을 운전할 수 있어야 합니다.

베이지안 딥러닝(Bayesian deep learning) 또는 베이지안 뉴럴넷(BNN, Bayesian neural network)은 결과뿐만 아니라 불확실성까지 추론할 수 있는 딥러닝 중 가장 유망한 방법론으로 여겨집니다. 이를 위해, 전통적인 딥러닝인 결정론적인 뉴럴넷(deterministic neural network)의 가중치는 단 하나의 값만을 사용하지만, BNN의 가중치는 확률 분포로 주어집니다.

BNN이 결과뿐만 아니라 불확실성까지 추정할 수 있다는 특징은 더 나은 판단을 내리는데 도움이 될 것입니다. 또한, BNN은 입력 데이터의 손상에 대해 더 강건합니다. 요약하면, BNN은 신뢰할 수 있는(trustworthy) 인공지능 시스템을 구축하는데 효과적입니다. 이밖에도, BNN은 예측 성능을 개선시거나, meta-learning에서 높은 성능을 보이는 등 다양한 장점을 갖고 있습니다.

하지만 베이지안 딥러닝의 추론 속도는 수십 배 느립니다

이런 장점에도 불구하고, BNN은 실용적인 도구로써 널리 사용되기에 치명적인 문제를 안고 있습니다. 이 문제는 바로 BNN은 결정론적인 딥러닝에 비해 추론 속도가 수십 배 느리다는 것입니다. 이는 BNN의 계산 비용이 수십 배 증가한다는 것을 뜻하기도 합니다.

우리는 이 포스트에서 이 문제를 해결하고자 합니다. 우선, 이 문제를 해결하기 위해서는 왜 BNN의 추론이 느린지 이해해야 합니다. 왜 이런 문제가 일어날까요?

베이지안 딥러닝 추론의 개략적인 설명

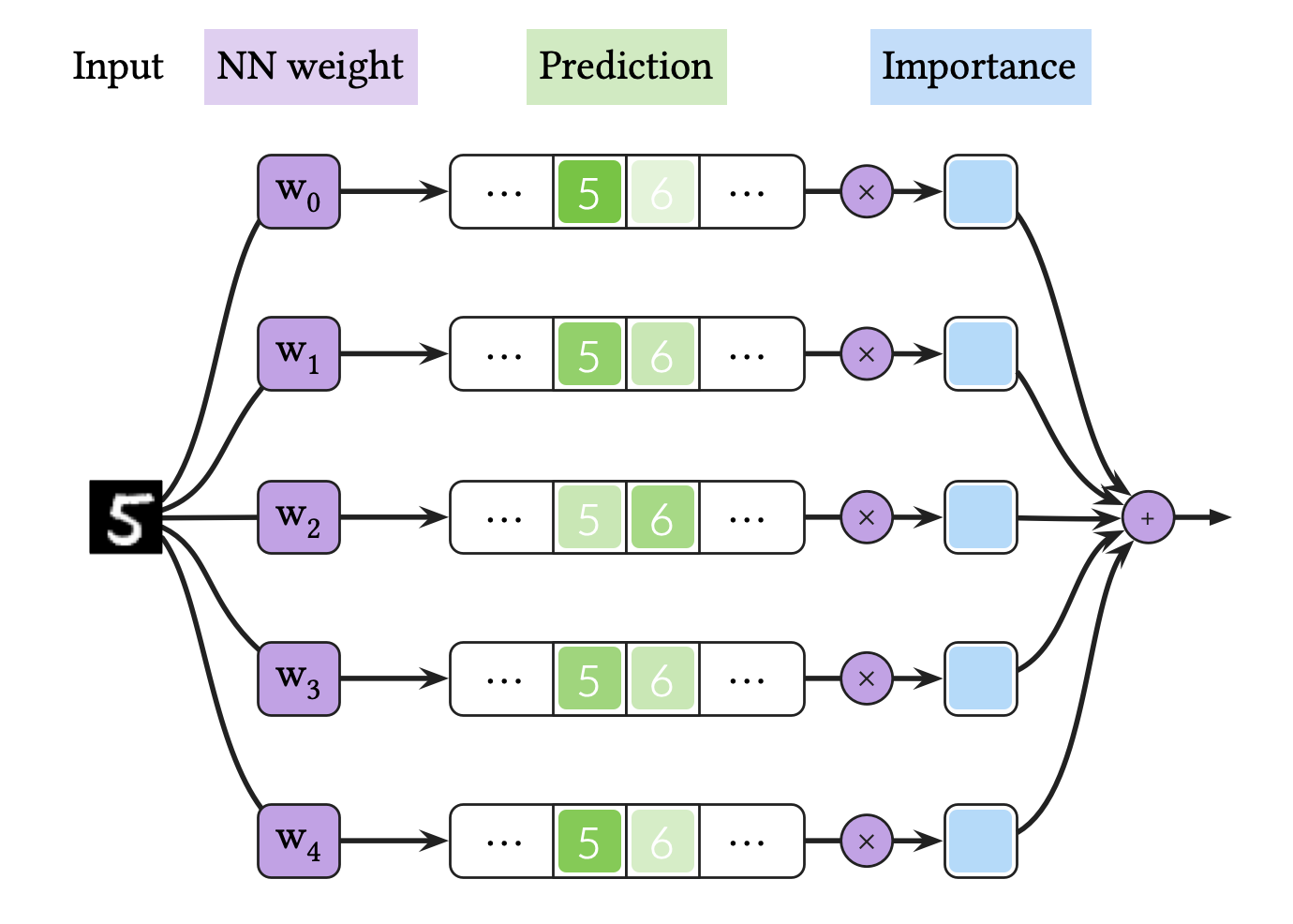
위의 그림은 BNN의 추론 과정을 도식화한 것입니다. BNN의 추론 과정은 다음과 같이 이뤄집니다.

1. 우리는 BNN의 학습 과정을 통해 뉴럴넷의 가중치(NN weight) 확률 분포를 얻었을 것입니다. 이 확률 분포로부터 여러 가중치를 샘플링해 뉴럴넷 앙상블을 구성합니다. 이 그림에서는 단순 예제로서의 이미지 분류를 위해 5개의 뉴럴넷 가중치를 사용해 5개의 뉴럴넷 앙상블을 구성했습니다.
2. 이 앙상블을 사용해 하나의 데이터에 대해 여러 확률 예측(prediction)을 구합니다. 예를들어, 이 그림에서는 5개의 예측(neural network logits)을 계산한 뒤, Softmax를 사용해 이를 확률로 변환해주었습니다. 만약 BNN으로 MC dropout을 사용한다면, 이 과정은 하나의 뉴럴넷을 사용해 하나의 데이터에 대해 여러 번 추론을 수행하는 것에 해당할 것입니다. 만약 BNN으로 Deep ensemble을 사용한다면, 각각의 서로 다른 뉴럴넷을 사용해 하나의 데이터에 대해 추론 결과를 도출하는 과정이 될 것입니다.
3. 이 확률 예측을 평균합니다. 위의 예에서는, 각 확률 예측에 동일한 중요도(importance) $\frac{1}{5}$를 곱한 후, 이들을 더합니다.

요약하면, BNN 추론 과정은 베이지안 뉴럴넷의 앙상블 평균입니다. 이 과정에서 뉴럴넷을 사용해 여러 번 추론하는 단계는 무엇보다 계산 부담이 상당히 큽니다. 따라서, BNN 추론에 소요되는 시간은 앙상블의 갯수에 비례해 증가합니다. 이 그림에서는 5개의 뉴럴넷을 사용했기 때문에 추론 속도는 5배 느려질 것입니다. 실제 응용 사례에서는, MC dropout의 경우 높은 예측 성능을 성취하기 위해서는 30번의 추론을 요구합니다. 따라서, MC dropout의 추론 속도는 결정론적인 딥러닝에 비해 30✕ 느려집니다.

베이지안 딥러닝 추론의 상세한 설명

이 과정을 좀 더 자세히 설명하겠습니다. BNN의 추론 결과는 다음과 같은 사후 예측 분포(PPD, posterior predictive distribution)로 주어집니다.

$$p(\textbf{y} \vert \textbf{x}_0, \mathcal{D}) = \int p(\textbf{y} \vert \textbf{x}_0, \textbf{w}) p(\textbf{w} \vert \mathcal{D}) d\textbf{w}$$

위 수식에서, $\textbf{x}_0$은 관측된 입력 데이터, $p(\textbf{y} \vert \textbf{x}_0, \textbf{w})$은 뉴럴넷의 예측, $p(\textbf{w} \vert \mathcal{D})$은 학습 데이터셋 $\mathcal{D}$가 주어졌을 때 뉴럴넷의 가중치 분포 (베이지안 통계에서의 posterior)를 뜻합니다.

이 식은 뉴럴넷 가중치에 대한 적분을 포함하고 있기 때문에, 일반적으로는 해석적으로 풀 수 없습니다. 따라서, 우리는 결과를 계산하기 위해 근사법을 도입해야 합니다. 가장 흔한 접근 방법은 아래와 같이 MC estimator라고 부르는, 적분을 합으로 근사하는 테크닉을 사용하는 것입니다.

$$p(\textbf{y} \vert \textbf{x}_0, \mathcal{D}) \simeq \sum_{\color{purple}{\textbf{w}_i}} \color{blue}{\frac{1}{N_{\textbf{w}}}} \color{green}{p(\textbf{y} \vert \textbf{x}_0, \textbf{w})}$$

위 수식에서 초록색은 예측 $\color{green}{p(\textbf{y} \vert \textbf{x}_0, \textbf{w})}$, 보라색은 뉴럴넷의 가중치 $\color{purple}{\textbf{w}_i}$, 파란색은 가중치의 중요도를 뜻합니다. 이는 앞선 그림과 같은 색상을 사용해 표시했으므로, 수식과 그림을 쉽게 비교해 보실 수 있습니다.

우리는 이 근사식을 위해 뉴럴넷 가중치 분포로부터 아래와 같은 $N_{\textbf{w}}$개의 iid 샘플을 사용했습니다.

$$\left( \color{purple}{\textbf{w}_i}, \color{blue}{\frac{1}{N_{\textbf{w}}}} \right) \sim \color{green}{p(\textbf{w} \vert \mathcal{D})}$$

위와 같이 MC estimator를 사용해 근사된 BNN의 사후 예측 분포를 계산하기 위해서는 $N_{\textbf{w}}$개의 뉴럴넷의 예측을 계산해야 합니다. 이는 결정론적인 딥러닝에 비해 BNN 추론을 $N_{\textbf{w}}$배 느리게 만듭니다.

어떻게 이와 같은 뉴럴넷 앙상블 평균을 효율적으로 계산함으로써 BNN 추론 속도를 향상시킬 수 있을까요?

벡터 양자화 베이지안 딥러닝은 사전에 기억된 예측을 사용함으로써 계산 속도를 향상시킵니다

우리는 BNN 추론이 심각하게 느리다는 단점을 극복하기 위해, 벡터 양자화 베이지안 딥러닝(VQ-BNN, vector quantized Bayesian neural network)을 제안합니다. VQ-BNN은 BNN과 달리 하나의 데이터에 대해 예측을 단 한 번만 계산합니다. 대신, 사전에 기억된 예측을 사용해서 이 결과를 보완합니다.

벡터 양자화 베이지안 딥러닝 추론의 개략적인 설명

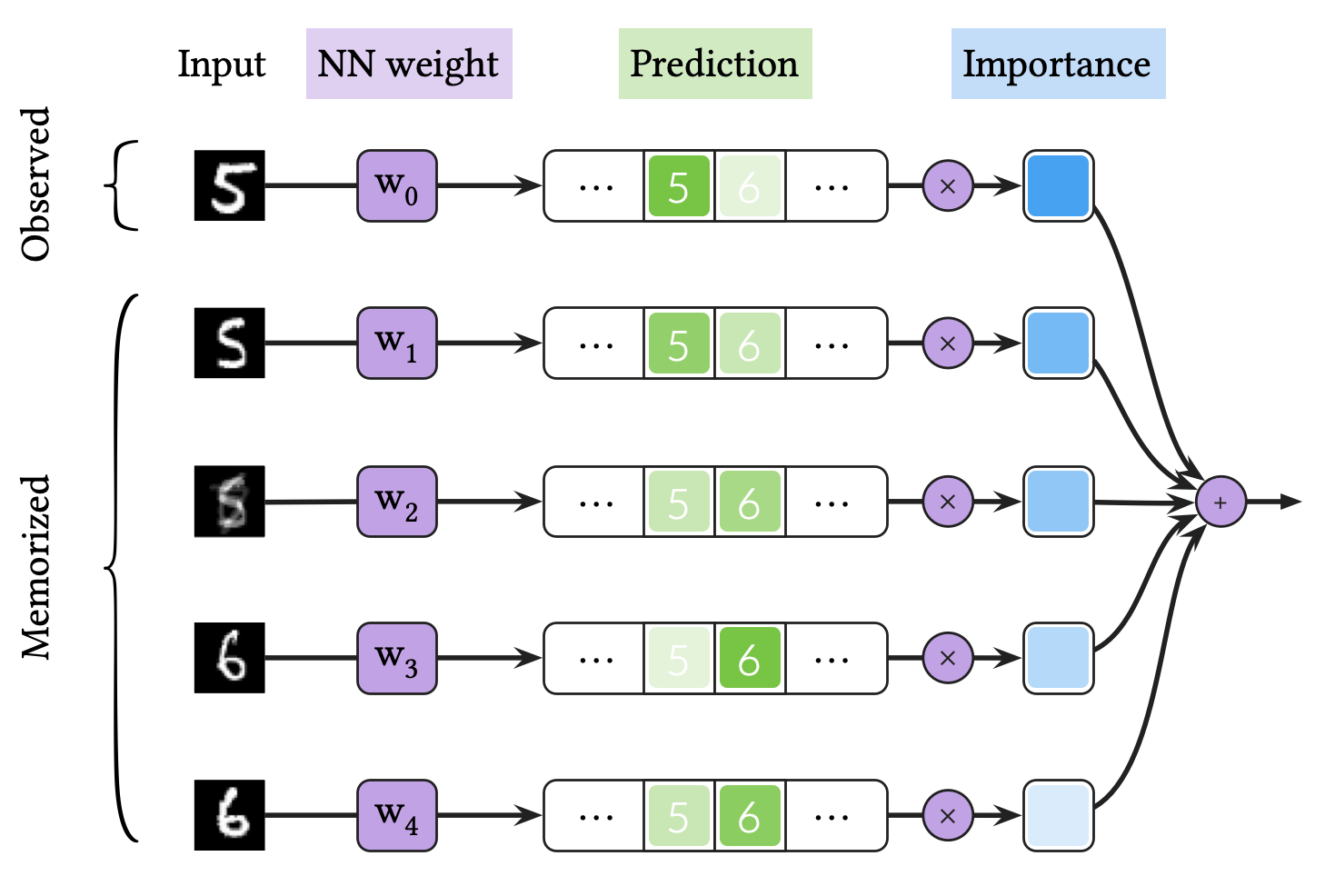
위의 그림은 VQ-BNN 추론 과정을 도식화한 것입니다. VQ-BNN 추론은 다음과 같이 수행됩니다.

1. 우선 우리는 BNN과 동일한 방식으로 가중치를 학습합니다. 이 학습 과정을 통해 얻은 뉴럴넷 가중치 확률분포로부터 하나의 가중치를 샘플링합니다. 그 다음, 이 가중치를 사용한 모델로 관찰된(observed) 입력 데이터에 대해 결과를 추론합니다.
2. 한편, 사전에 여러 입력과 여러 가중치에 대해 결과를 추론했었고, 이를 기억하고 있다고 합시다. 우리는 기억된 입력 데이터에 대한 중요도(importance)를 계산합니다. 이 중요도는 관찰된 입력 데이터와 기억되어있는 입력 데이터간의 유사도를 기반으로 정의됩니다.
3. 이 중요도를 사용해서 관찰된 입력 데이터에 대한 새로운 예측과 기억되어져있는 예측을 가중 평균함으로써 최종 결과를 계산합니다.

요약하면, VQ-BNN 추론은 관찰된 입력에 대한 새로운 예측과 저장되어져있는 예측들간의 앙상블 중요도 가중 평균입니다. 즉, VQ-BNN은 결과를 과거에 기억된 결과들로 보완하는 과정이라고 할 수 있습니다. 이 과정에서 가장 계산 부담이 큰 단계는 관측된 입력에 대해 새로운 예측을 계산하는 부분입니다. 만약 중요도를 유도하는 부분의 계산 부담이 무시할만하다면, VQ-BNN 추론 속도는 결정론적인 딥러닝의 추론 속도와 거의 같습니다.

벡터 양자화 베이지안 딥러닝 추론의 상세한 설명

이를 좀 더 상세하게 설명해 보겠습니다. 우리는 BNN에서 사용하는 하나의 관측된 데이터 포인트 $\textbf{x}_0$에 대한 PPD 대신, 아래와 같은 여러 데이터의 집합 $\mathcal{S}$에 대한 PPD를 새롭게 제안합니다.

$$p(\textbf{y} \vert \mathcal{S}, \mathcal{D}) = \int p(\textbf{y} \vert \textbf{x}, \textbf{w}) \, p(\textbf{x} \vert \mathcal{S}) \, p(\textbf{w} \vert \mathcal{D}) \, d\textbf{x} d\textbf{w}$$

우리는 여기서 우변에 데이터의 분포 $p(\textbf{x} \vert \mathcal{S})$를 도입했습니다. 예를들어, $\mathcal{S}$가 시간에 대해 불변인 소스(source)로부터 유래한 것이라면, 이 분포는 관측 오차가될 수 있을 것입니다. 만약 $\mathcal{S}$가 동일한 데이터로 구성되어 있어서 $p(\textbf{x} \vert \mathcal{S}) = \delta(\textbf{x} - \textbf{x}_0)$라면 이 식은 BNN 추론의 PPD와 동일해집니다.

이 식은 아래와 같이 쓸 수도 있습니다.

$$p(\textbf{y} \vert \mathcal{S}, \mathcal{D}) = \int p(\textbf{y} \vert \textbf{x}, \textbf{w}) \, p(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D}) \, d\textbf{x}d\textbf{w}$$

이 식에서 우리는 편의를 위해 $p(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D}) = p(\textbf{x} \vert \mathcal{S}) \, p(\textbf{w} \vert \mathcal{D})$를 도입했습니다. 그러면 이 새로운 PPD의 데이터 $\textbf{x}$와 뉴럴넷의 가중치 $\textbf{w}$는 대칭성을 갖고 있음을 보다 쉽게 알아챌 수 있습니다.

BNN과 마찬가지로, 이 적분식 또한 해석적으로 풀 수 없습니다. 따라서 우리는 이 식을 계산하기 위해 근사법을 도입해야 합니다. 단, 여기서 우리는 iid 샘플을 사용하는 MC estimator를 사용하지 않습니다. 대신, 우리는 중요도 샘플링(importance sampling)을 사용해 이를 아래와 같이 근사합니다.

$$p(\textbf{y} \vert \mathcal{S}, \mathcal{D}) \simeq \sum_{\color{purple}{\left( \textbf{x}_{i}, \textbf{w}_{i} \right)}} \color{blue}{\pi(\textbf{x}_{i}, \textbf{w}_i \vert \mathcal{S}, \mathcal{D})} \, \color{green}{p(\textbf{y} \vert \textbf{x}_{i}, \textbf{w}_{i})}$$

이와 같이 근사하기 위해 우리는 아래와 같은 샘플과 중요도를 사용했습니다.

$$\left( \color{purple}{(\textbf{x}_{i}, \textbf{w}_{i})}, \color{blue}{\pi(\textbf{x}_{i}, \textbf{w}_{i} \vert \mathcal{S}, \mathcal{D})} \right) \sim \color{green}{p(\textbf{x}_{i}, \textbf{w}_{i} \vert \mathcal{S}, \mathcal{D})}$$

이 수식에서, 초록색은 예측 $\color{green}{p(\textbf{y} \vert \textbf{x}_0, \textbf{w})}$, 보라색은 데이터와 뉴럴넷의 가중치 튜플 샘플 $\color{purple}{(\textbf{x}_i, \textbf{w}_i)}$, 파란색은 샘플의 중요도 $\color{blue}{\pi(\textbf{x}_{i}, \textbf{w}_i \vert \mathcal{S}, \mathcal{D})}$를 나타냅니다. 마찬가지로, 색깔을 이용해서 동일한 요소들끼리 그룹을 지어놓았으므로 위의 VQ-BNN 추론을 묘사한 그림과 비교해보시기 바랍니다.

왜 우리는 굳이 BNN 추론을 근사할때처럼 iid 샘플을 사용하지 않고, 중요도 샘플링을 사용할까요? 우리는 적분을 근사하기 위해 확률 분포를 여러 개의 벡터들로 표현해야 합니다. 이를 위해, 벡터 샘플들은 고정시킨 채로 중요도만을 변경해서 확률 분포를 근사하는 관점을 사용할 것입니다. 이런 관점을 따라, 우리는 벡터 샘플을 프로토타입(prototype), 또는 양자화된 벡터(quantized vector)라고 부릅니다.

이제 우리는 위에서 제시한 VQ-BNN을 이용해 추론 속도를 개선시킬 수 있습니다. VQ-BNN의 PPD의 합을 첫번째 항과 나머지로 나눠보겠습니다. 일반성을 잃지 않고, 첫번째 항 $\ \pi(\textbf{x}_{i}, \textbf{w}_{i} \vert \mathcal{S}, \mathcal{D}) \, p(\textbf{y} \vert \textbf{x}_{0}, \textbf{w}_{0})$의 데이터$\textbf{x}_0$를 관측 데이터라고 둘 수 있습니다. 우리는 이 항만을 뉴럴넷을 통해 새롭게 계산하겠습니다. 그리고 나머지 항들 $\sum_{i = 1}^{N_{\textbf{w}}} \pi(\textbf{x}_{i}, \textbf{w}_{i} \vert \mathcal{S}, \mathcal{D}) \, p(\textbf{y} \vert \textbf{x}_{i}, \textbf{w}_{i})$은 사전에 기억된 데이터와 추론에서 가져오겠습니다. 그러면 VQ-BNN 추론은 단지 관측 데이터에 대해 한 번 뉴럴넷 추론을 실행하는 것과 같은 시간이 걸립니다.

중요도를 $\textbf{x}$에만 의존하도록 단순화하기 (옵션). 각 샘플의 중요도는 $\pi(\textbf{x}_{i}, \textbf{w}_{i} \vert \mathcal{S}, \mathcal{D})$와 같이 데이터$\textbf{x}$뿐만 아니라 뉴럴넷 가중치 $\textbf{w}$에도 의존하도록 표현되어져 있습니다. 하지만, 사실 이 중요도는 뉴럴넷 가중치에는 의존하지 않습니다. 즉, $\pi(\textbf{x}_{i}, \textbf{w}_{i} \vert \mathcal{S}, \mathcal{D}) = \pi(\textbf{x}_{i} \vert \mathcal{S})$입니다. 따라서, 우리는 가중치를 계산할 때 모델의 특성을 고려할 필요 없이 데이터간의 유사도만을 고려하면 됩니다.

그 이유는 다음과 같습니다. 데이터와 뉴럴넷 가중치 샘플 $\{ (\textbf{x}_i, \textbf{w}_i) \}$의 확률 분포 $f(\textbf{x}, \textbf{w})$를 정의합시다. 즉, $(\textbf{x}_i, \textbf{w}_i) \sim f(\textbf{x}, \textbf{w})$입니다. 우리는 이를 사용해 $p(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D}) = \frac{p( \textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D})}{f( \textbf{x}, \textbf{w})} f( \textbf{x}, \textbf{w})$로 쓸 수 있습니다. 이 식을 가중치 샘플링과 비교함으로써 $\pi( \textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D}) = \frac{p( \textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D})}{f(\textbf{x}, \textbf{w})}$임을 얻을 수 있습니다.

한편, 뉴럴넷 가중치 샘플 $\{ \textbf{w}_i \}$이 posterior $p( \textbf{w} \vert \mathcal{D})$를 따르며 iid라고 합시다. 그러면, 우리는 $f(\textbf{x}, \textbf{w})$를 posterior와 $\textbf{x}$에만 의존하는 확률 분포 $g(\textbf{x})$로, 즉 $f(\textbf{x},\textbf{w}) = g(\textbf{x}) \, p(\textbf{w} \vert \mathcal{D})$와 같이 분리할 수 있습니다. 정의에 의해 $p(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D}) = p(x \vert \mathcal{S}) \, p(\textbf{w} \vert \mathcal{D})$이며, $\pi(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D}) = \frac{p(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D})}{f(\textbf{x}, \textbf{w})} = \frac{p(\textbf{x} \vert \mathcal{S})}{g(\textbf{x})}$가 성립합니다. 우리는 $\frac{p(\textbf{x} \vert \mathcal{S})}{g(\textbf{x})}$를 $\textbf{x}$에만 의존하는 중요도 $\pi(\textbf{x} \vert \mathcal{S})$로 새롭게 정의합니다.

VQ-BNN의 의미를 단순한 예제를 통해 이해하기

VQ-BNN의 성질을 더 깊이 이해하기 위해 한 가지 실험을 수행하겠습니다. 이 실험은 노이즈를 포함한 입력 데이터 $\textbf{x}$의 시퀀스 $\mathcal{S}$가 순차적으로 주어졌을 때 뉴럴넷 가중치 $\textbf{w}$를 사용해 $\textbf{y}$를 예측하는 것입니다.

이 실험에서 우리는 다음과 같은 네 가지 방식을 비교합니다. 첫번째는 결정론적인 뉴럴넷(DNN, deterministic neural network)입니다. 두번째는 BNN입니다. 세번째는 DNN에 VQ-BNN을 적용시킨 것으로, 우리는 이를 VQ-DNN이라고 부르겠습니다. 즉, VQ-DNN은 추론 과정에서 하나의 뉴럴넷 가중치를 사용하지만, 여러 데이터에 대해 사전에 기억된 예측을 사용해 이를 보완하는 방식입니다. 마지막은 VQ-BNN입니다. VQ-BNN은 여러 뉴럴넷 가중치를 사용하며, 동시에 여러 데이터에 대해 사전에 기억된 예측을 사용해 예측을 보완합니다.

DNN	BNN	VQ-DNN	VQ-BNN

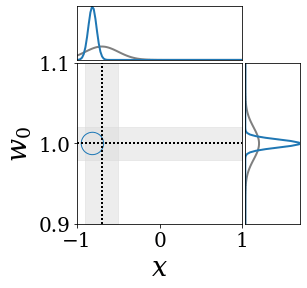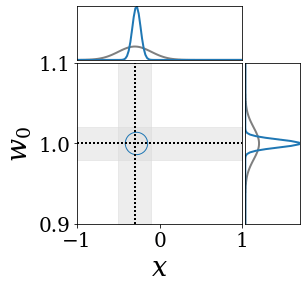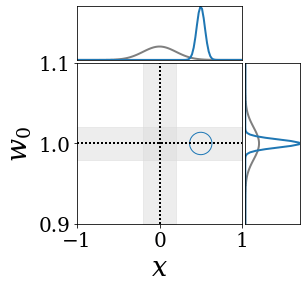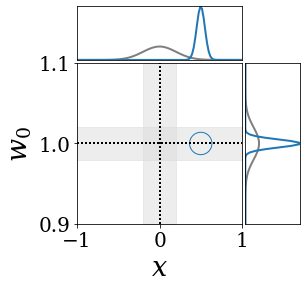
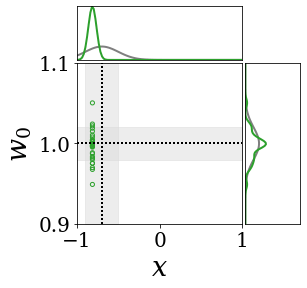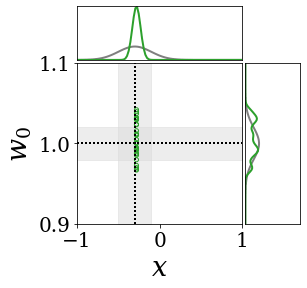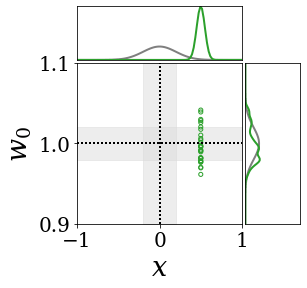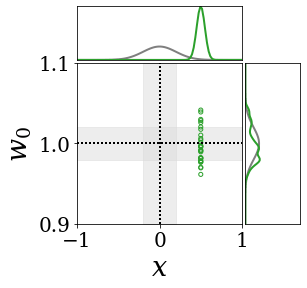
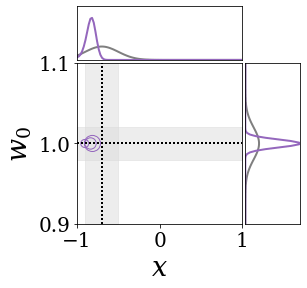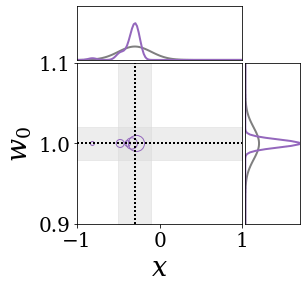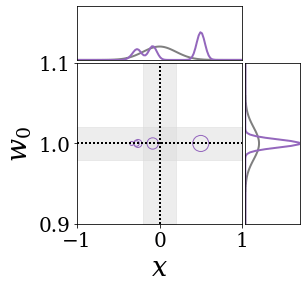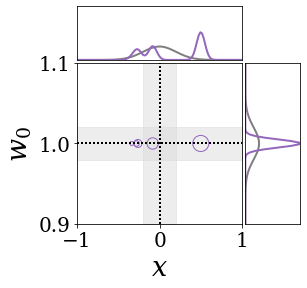
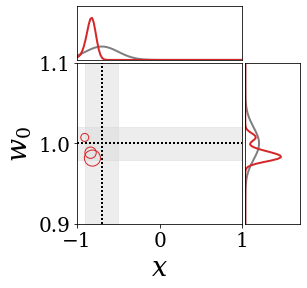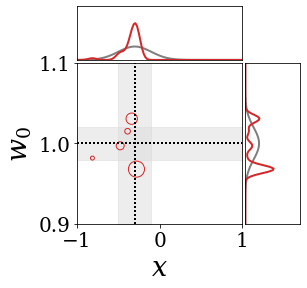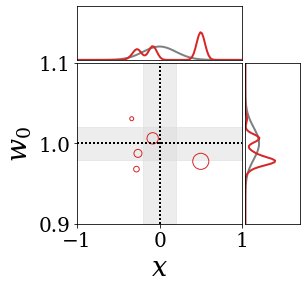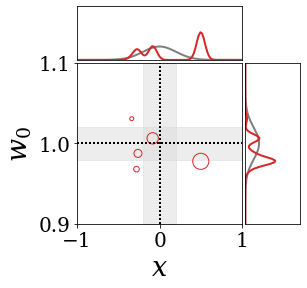
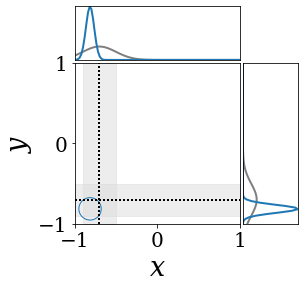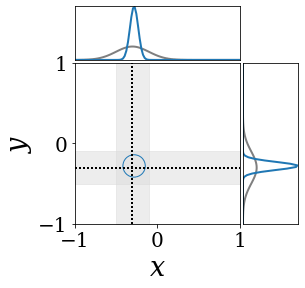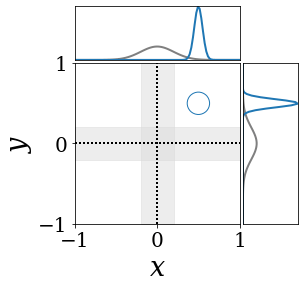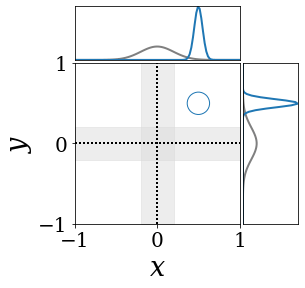
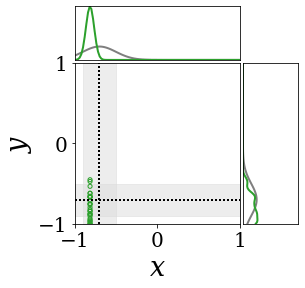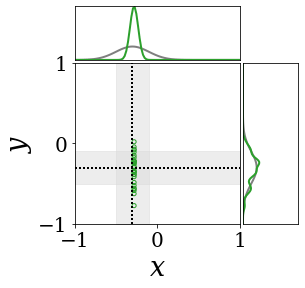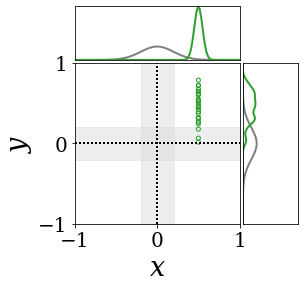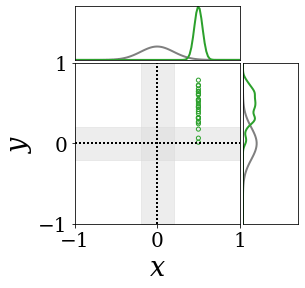
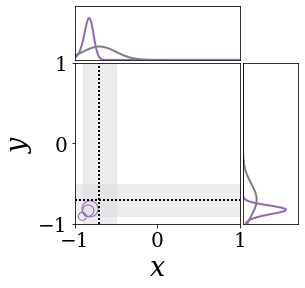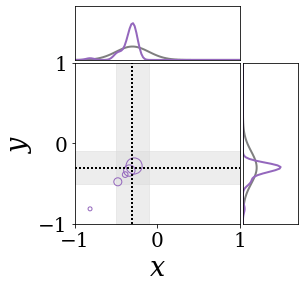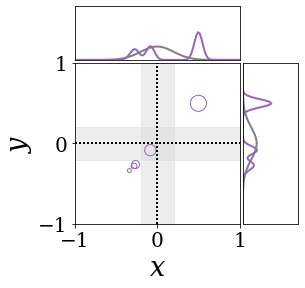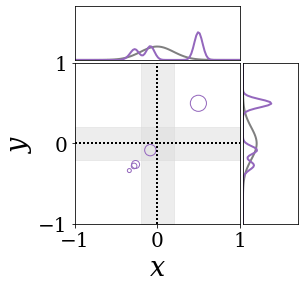
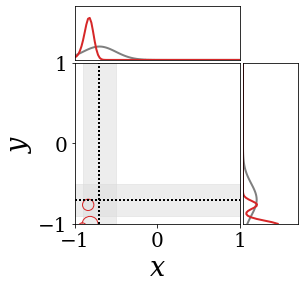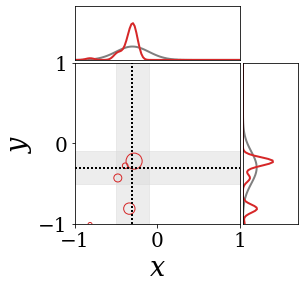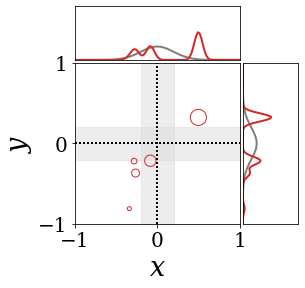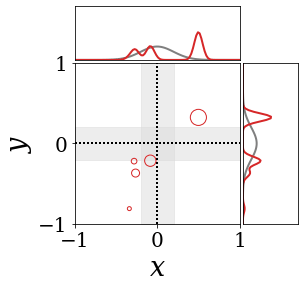
위의 그림은 각 방법에 대해 샘플들로 근사한 $p(\textbf{x}, \textbf{w} \vert \mathcal{S}, \mathcal{D})$와 $p(\textbf{x}, \textbf{y} \vert \mathcal{S}, \mathcal{D})$이 순차적으로 변하는 과정을 표현한 것입니다. 여기서 각 동그라미는 샘플을 뜻하며, 동그라미의 크기는 해당 샘플의 중요도를 나타냅니다. 이 그림은 동시에 이들의 marginal distribution인 $p(\textbf{x} \vert \mathcal{S})$, $p(\textbf{w} \vert \mathcal{D})$, $p(\textbf{y} \vert \mathcal{S}, \mathcal{D})$도 표현하고 있습니다. 검은 점선과 회색의 분포는 참값을 나타냅니다.

이 결과는 DNN, BNN, VQ-DNN, VQ-BNN의 특징을 보여줍니다. 우선, DNN은 결과를 예측하기 위해 하나의 데이터와 하나의 뉴럴넷 가중치를 사용합니다. BNN은 하나의 데이터를 사용하지만, 뉴럴넷 가중치 분포를 사용합니다. VQ-DNN은 DNN과 같이 하나의 뉴럴넷 가중치를 사용하지만, 여러 데이터에 대한 예측을 사용해 결과를 예측합니다. VQ-BNN은 뉴럴넷 가중치 분포를 사용하며, 동시에 여러 데이터에 대한 예측도 사용합니다.

BNN과 VQ-BNN은 각각의 샘플을 다루는 방식에도 차이를 보입니다. BNN은 서로 다른 데이터 $\textbf{x}$에 대해 항상 서로 다른 뉴럴넷 가중치 $\textbf{w}$를 샘플링합니다. 이는 결과를 추론하기 위해 하나의 입력과 각각의 가중치에 대해 매번 새로운 예측을 수행해야 한다는 것을 뜻합니다. 반면, VQ-BNN은 과거에 주어진 $( \textbf{x}, \textbf{w}, \textbf{y})$ 벡터 프로토타입들은 고정시킨 채로, 이들의 중요도를 조절하는 방식으로 결과를 유도합니다.

이 애니메이션의 마지막 프레임에 주어진 데이터는 이상치(outlier)를 나타냅니다. 이때의 참값은 $\textbf{x}_{\text{true}}=0$이지만, 주어진 데이터는 $\textbf{x}=0.4$입니다. DNN과 BNN은 이 잡음이 낀 데이터에만 의존해 $\textbf{y}$를 예측합니다. 따라서, DNN과 BNN의 예측치는 참값과 비교할 때 부정확합니다. 반면, VQ-DNN과 VQ-BNN은 이상치뿐만 아니라 이상치와 유사한 이전의 데이터에 대한 예측을 동시에 사용해 $\textbf{y}$를 예측합니다. 따라서, VQ-DNN과 VQ-BNN은 이상치 데이터가 주어지더라도 더욱 정확하고 강건한 예측을 수행할 수 있습니다.

VQ-BNN을 실제 세계에 적용하기

실제로 VQ-BNN을 적용하려면 어떤 프로토타입 벡터를 사용할 것인지, 그 프로토타입 벡터의 중요도를 어떻게 결정할 것인지 결정해야 합니다. 계산의 효율성을 위해, 프로토타입 벡터는 관측된 데이터와 유사한 데이터들로 구성되어야 하며, 중요도는 계산 복잡도가 높지 않아야 합니다.

데이터 스트림 분석, 특히 동영상에 대한 데이터 처리는 추론 속도가 중요한 분야입니다. 우리는 동영상 데이터에 대해 VQ-BNN을 적용시키기 위해 데이터 스트림의 시간적 일관성(temporal consistency)을 활용하는 테크닉을 제시했습니다. 그리고 semantic segmentation 예제를 통해 VQ-BNN의 계산 속도는 결정론적 딥러닝과 비슷하며 BNN보다 최대 30✕ 빠르다는 것을 실험적으로 보였습니다. 이 예제에서, VQ-BNN의 예측 성능은 BNN과 동등하거나 그 이상이었습니다. Semantic segmentation과 같은 실제 세계의 문제를 풀기 위해 VQ-BNN을 사용한 사례는 시간적 평활화를 사용한 효율적인 불확실성 예측을 참고해 주시기 바랍니다.

더 읽을거리

• 이 포스트는 논문 “Vector Quantized Bayesian Neural Network Inference for Data Streams”을 기반으로 작성되었습니다. VQ-BNN에 대한 더욱 엄밀하고 자세한 사항은 해당 논문을 참고해주시기 바랍니다. VQ-BNN의 구현은 GitHub을 참고해주시기 바랍니다. 만약 이 포스트나 논문이 유용하다고 생각하신다면, 위 논문을 인용해주시면 감사하겠습니다. 이와 관련된 첨언이나 피드백이 있으시다면, 편하게 연락해 주시기 바랍니다.