TL; DR
스칼라 클래스를 프로그래밍하기 어려우시다면 다음 순서대로 디자인하세요.
- 데이터를 선언하고 구현하세요
- 프로그램이 요구하는 연산을 나열하고, 기본 연산과 기본 연산에서 유도된 연산을 구분하세요
- 연산 호출의 단순화를 위한 편의성 문법을 추가하세요
스칼라 클래스, 어디서부터 어떻게 디자인해야 할까요?
스칼라의 문법을 공부한 뒤 처음 실용적인 프로그램을 만드려고 하면, 어디서부터 시작해야 할 지 막막합니다. 언제 trait을 써야 하고, 언제 class와 abstract class를 사용해야 할까요? 언제 object를 사용해야 할까요? 메소드는 어떤 식으로 정의해야 할까요? 어떻게 클래스를 디자인하고 언제 상위 클래스를 상속해야 할까요? 상속 대신 구성하라는 원칙이 스칼라에서 어떻게 받아들여질까요?
스칼라는 함수형 프로그래밍 언어이기도 하고, Java와의 호환성을 위해 객체 지향 프로그래밍 언어이기도 합니다. 스칼라는 서로 다른 두 가지 패러다임을 지원하기 위해, 언어가 지원하는 자유도가 굉장히 높은 편입니다. 하지만, 처음 스칼라로 프로그래밍을 하는 입장에서는 수많은 선택권이 오히려 혼란을 가져오기도 합니다. 이 포스팅에서는 함수형 언어로서 스칼라를 사용하기 위해, 스칼라의 클래스를 작성할 때 일반적으로 사용할 수 있는 형식을 제시하려고 합니다. 이 형식은 스칼라의 클래스를 좀 더 체계적으로 다룰 수 있으므로, 가독성을 높이고 보다 확장 가능한 프로그램을 작성할 수 있도록 돕습니다.
FizzBuzz 테스트
FizzBuzz 테스트는 프로그래머의 채용 문제로 널리 알려져 있습니다. 이를 간략히 요약하면 다음과 같습니다.
1부터 100까지의 숫자를 출력하라. 단, 3의 배수들은 “Fizz”, 5의 배수들은 “Buzz”, 3과 5의 배수들은 “FizzBuzz”라는 문자열로 치환하라.
FizzBuzz 테스트를 1분 안에 풀기 위한 가장 단순한 해법은 다음과 같습니다.
val input = (1 to 100).toList
val output = input.map {
case i if i % 15 == 0 => "FizzBuzz"
case i if i % 3 == 0 => "Fizz"
case i if i % 5 == 0 => "Buzz"
case i => i.toString
}
하지만, 만약 이 해법이 실제로 상용 프로그램에 사용되는 코드 조각이라면, 여기서 끝내서는 곤란합니다. 이 단순한 해법을 리팩토링함으로써, 스칼라 클래스를 작성할 때 일반적으로 사용할 수 있는 형식에 대해 소개하겠습니다.
FizzBuzz 테스트 자세히 들여다보기
FizzBuzz 테스트를 메시지(문자메시지라고 생각해도 좋고, 네트워크 메시지라고 생각해도 좋습니다)를 다루는 문제로 생각합시다. 그러면, FizzBuzz 테스트는 모든 미가공된 데이터(raw data)에 대해 다음과 같은 연산 과정을 수행하는 것으로 바라볼 수 있습니다.
- 미가공된 데이터(여기서는 숫자)를 숫자를 포함하는 메시지로 변환
- 숫자를 포함하는 메시지에 대해 다음을 수행
-
- 만약 메시지의 숫자가 3과 5의 배수라면, "FizzBuzz"를 포함한 메시지로 변환
- 위의 조건에 해당되지 않으면서, 만약 메시지의 숫자가 3의 배수라면, "Fizz"를 포함한 메시지로 변환
- 위의 조건에 해당되지 않으면서, 만약 메시지의 숫자가 5의 배수라면, "Buzz"를 포함한 메시지로 변환
- 위의 어떤 조건에도 해당되지 않으면, 메시지를 그대로 유지
- 메시지를 문자열로 변환
정리하면, 우리는 숫자와 문자열을 포함하는 메시지 클래스(Msg라고 부릅시다)를 구현해야 하고, 이 메시지 클래스에 대해 다음의 다섯 가지 기능을 구현해야 합니다.
- 미가공 데이터를 메시지로 변환하는 기능
- 미가공 데이터의 조건을 검증하는 기능
- 조건에 해당되지 않으면, 다음 조건의 검증으로 넘어가는 기능
- 미가공 데이터의 내용을 변환하는 기능
- 메시지를 문자열로 변환하는 기능
여기에 더해, 미가공 데이터를 포함하지 않는 메시지(EmptyMsg)를 구현하기로 합시다. EmptyMsg는 위의 연산 과정에 직접적으로 드러나지는 않았습니다. 하지만, 미가공 데이터를 메시지로 변환할 때 실패하는 등, 메시지를 다루는 과정에서 연산이 실패한 경우 어떤 결과를 내놓아야 할 지 생각하면, 이미 위의 전체 과정이 EmptyMsg를 구현해야 한다는 것을 암시하고 있습니다.
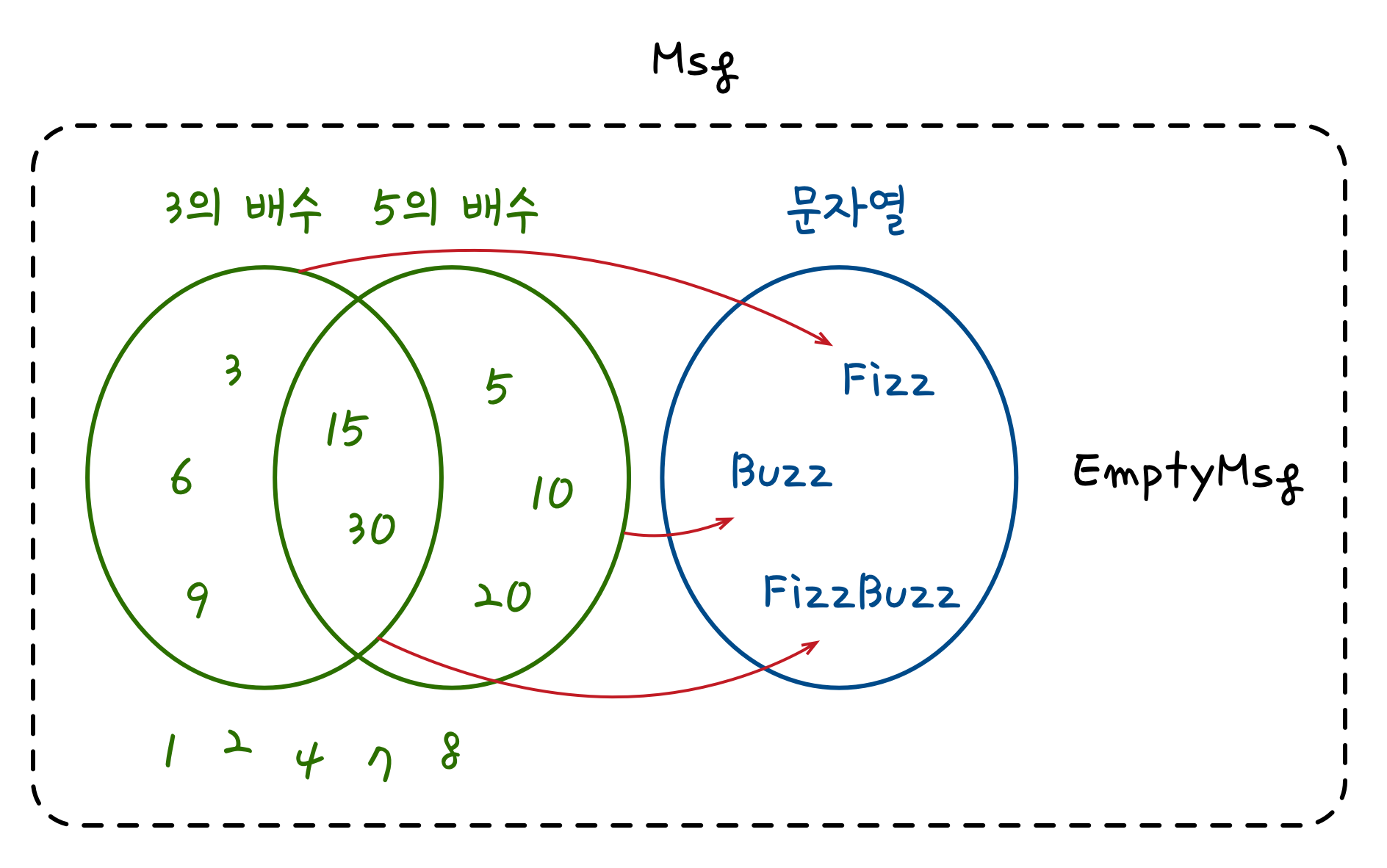
위 그림은 앞서 언급한 여러 종류의 Msg를 벤 다이어그램으로 표기한 것입니다. 우선, 숫자를 포함하는 메시지(초록색 원과 숫자)은 4가지 카테고리로 분류할 수 있습니다. 이는 각각 3의 배수, 5의 배수, 3과 5의 배수, 그 이외의 것입니다. FizzBuzz 테스트는 앞선 3개의 카테고리를 각각 “Fizz”, “Buzz”, “FizzBuzz”가 포함된 문자열 메시지(파란색 원과 문자열)로 변환(빨간색 화살표)하기를 요구합니다. 한편, EMptyMsg도 Msg의 한 종류이므로 Msg의 하위 카테고리로 정의되어야 합니다.
데이터와 생성자
FizzBuzz 테스트에서 다루는 데이터인 숫자와 문자열을 포함하는 Msg와 아무것도 포함하지 않는 EmptyMsg를 구현해 보겠습니다. 이것은 프로그래밍에서 자료 구조에 대응됩니다. 즉, 이 섹션에서 소개하는 형식은 메모리나 디스크에 유지하기 위한 데이터에 일반적으로 적용할 수 있습니다. 또, 수학에서 숫자, 삼격형, 행렬과 같은 수학적 대상을 구현하는데 적용할 수 있습니다.
숫자와 문자열을 포함하는 Msg를 구현하기 위해, 임의의 타입 A를 포함하는 Msg[A]를 제네릭 클래스를 이용해 선언하겠습니다. 그러면 Msg는 숫자와 문자열은 물론, 임의의 타입의 미가공 데이터를 포함할 수 있습니다. 그리고 Msg를 A에 대해 공변(Covariant)하도록 하겠습니다. 이 뜻은, 임의의 T의 하위 타입(subtype) U가 존재한다면, Msg[U] 또한 Msg[T]의 하위 타입이라는 뜻입니다. 이를 이용해, 모든 타입에 대한 하위 타입인 Nothing을 이용해 EmptyMsg를 선언하겠습니다.
trait Msg[+A]
trait EmptyMsg extends Msg[Nothing]
이제 EmptyMsg는 모든 타입 A에 대한 Msg[A]의 하위 타입입니다.
다음으로, Msg[A]와 EmptyMsg를 생성할 수 있는 방법도 정의되어야 할 것입니다. 이를 다음과 같이 object를 이용해 정의합니다.
object Msg {
private case class MsgImpl[A](a: A) extends Msg[A]
private case object EmptyMsgImpl extends EmptyMsg
def apply[A](a: A): Msg[A] = MsgImpl(a)
def empty: EmptyMsg = EmptyMsgImpl
}
이제 Msg를 Msg(2), Msg("Fizz"), Msg.empty와 같이 생성할 수 있습니다.
여기서 Msg를 class나 case class로 선언하는 대신 trait으로 선언하고, 실제 구현인 case class는 object Msg에 숨겼습니다. 이렇게 한 이유는 Msg가 상속(extends)될 수 있다는 가능성을 열어두기 위해서입니다. 다른 말로 하면, trait Msg은 이것의 하위 타입이 존재할 수도 있다는 암시를 주고 있습니다. 실제로 EmptyMsg는 Msg의 하위 타입이기도 합니다. 더 나아가, Msg에 새로운 성질을 부여한 하위 타입을 새로 정의할 수도 있습니다. 예를 들면, timestamp가 포함된 Msg를, Msg를 상속함으로써 정의할 수 있습니다.
이 선언을 앞선 섹션에서 소개한 소개한 Msg의 벤 다이어그램과 비교함으로써 상속과 카테고리의 관계에 대해서 생각해 볼 수 있습니다. EmptyMsg를 Msg를 상속해 구현한다는 것은 EmptyMsg가 Msg의 하위 카테고리, 또는 Msg의 부분집합이라는 것과 동등합니다. 여기서 소개한 형식을 따른다면, 여러 클래스의 상속관계만을 파악함으로써, 클래스가 어떤 관계에 있는지 알 수 있습니다. 따라서, 이 형식은 상속을 적극적으로 권장합니다.
주의할 것은 Msg를 어떻게 다루는지를 trait Msg에 정의하지 않는다는 것입니다. 여기서 소개하는 형식은 Msg를 어떻게 보관할지와 어떻게 다룰지를 분리합니다.
기본 연산과 파생된 성질들
앞서 Msg 클래스를 통해 FizzBuzz 테스트에서 다루는 미가공 데이터를 어떻게 보관할 지 정했으니, 이제 Msg 클래스를 어떻게 다룰지 선언하겠습니다. Msg 클래스가 자료 구조에 대응됐다면, 이 선언은 자료 구조를 다루는 알고리즘에 대응됩니다.
앞선 섹션에서 FizzBuzz 테스트를 위해 다음 다섯 가지 기능이 요구된다고 언급한 적 있습니다.
- 미가공 데이터를 메시지로 변환하는 기능
- 미가공 데이터의 조건을 검증하는 기능
- 조건에 해당되지 않으면, 다음 조건의 검증으로 넘어가는 기능
- 미가공 데이터의 내용을 변환하는 기능
- 메시지를 문자열로 변환하는 기능
이 기능들을 구현하기 위해 point, filter, orElse, map, show라는 다섯 가지 연산을 도입하겠습니다.
point연산은 임의의 타입A의 미가공 데이터를 메시지로 변환하는 함수입니다.filter연산은Msg에 포함된 미가공 데이터를 주어진 조건에 대해 검증합니다. 만약 검증 결과가true라면Msg를 그대로 반환하고,false라면EmptyMsg를 반환합니다.orElse연산은 두 개의Msg를 취합니다. 만약 첫 번째Msg가EmptyMsg가 아니라면, 첫 번째Msg를 반환합니다. 만약 첫 번째Msg가EmptyMsg이라면, 두 번째Msg를 반환합니다.map연산은Msg에 포함된 미가공 데이터를 변경합니다.show연산은Msg를 문자열로 변환합니다.
우리는 이 다섯 가지 연산에서 다음을 관찰할 수 있습니다. 우선, orElse 연산은 패턴매치로 정의할 수 있습니다. 두 번째로, filter와 map 연산은 Msg를 변경하는 연산이므로, 공통점이 있는 것처럼 보입니다.
filter와 map을 구현하기 위해, flatMap이라는 연산을 도입하겠습니다. flatMap은 Msg의 미가공 데이터를 다른 Msg로 변환하는 함수를 변수로 취합니다. 만약 이 함수의 연산 결과가 EmptyMsg이라면 flatMap의 결과로 EmptyMsg을 반환합니다. 만약 그렇지 않다면, 그 결과를 반환합니다.
이제 이 연산들을 두 가지 그룹으로 구분하겠습니다. 우선, point, flatMap, show는 기본 연산(elementary operations)입니다. 반면, map, filter, orElse는 기본 연산으로부터 유도된 연산입니다. 이들은 기본 연산들의 조합으로 표현할 수 있거나, Msg의 선언으로부터 자연히 정의될 수 있습니다.
이 연산들을 다음과 같이 선언하겠습니다.
trait MsgOps extends MsgLaws {
def point[A](a: A): Msg[A]
def flatMap[A, B](msg: Msg[A], f: A => Msg[B]): Msg[B]
def show[A](msg: Msg[A]): String
}
trait MsgLaws { self: MsgOps =>
def map[A, B](msg: Msg[A], f: A => B): Msg[B] =
flatMap(msg, (a: A) => point(f(a)))
def filter[A](msg: Msg[A], f: A => Boolean): Msg[A] =
flatMap(msg, (a: A) => if(f(a)) msg else Msg.empty)
def isEmpty[A](msg: Msg[A]): Boolean =
msg match {
case _: EmptyMsg => true
case _ => false
}
def orElse[A, B >: A](msg1: Msg[A], msg2: Msg[B]): Msg[B] =
if(!isEmpty(msg1)) msg1 else msg2
}
이 선언에서 MsgOps는 기본 연산을 선언한 trait이고, MsgLaws는 기본 연산으로부터 유도된 연산을 선언하고 구현한 trait입니다. trait Msg와 마찬가지로, 연산을 정의한 MsgOps 클래스도 상속될 수 있음을 암시하기 위해 trait으로 선언되었습니다. 위에서 보듯이, MsgOps에 선언된 세 가지 연산만을 정의하면 자연스럽게 MsgLaws도 정의될 수 있음을 표현하고 있습니다. 따라서, 하위 클래스에서 MsgOps를 상속한 뒤 기본 연산만을 정의함으로써, 기본 연산에서 유도된 다양한 성질을 사용할 수 있습니다. Msg가 수학에서 수학적 대상에 대응됐다면, MsgOps는 공리(axiom)에, MsgLaws는 정리(theorem)에 대응됩니다.
여기서 MsgOps는 MsgLaws를 상속하고, MsgLaws는 MsgOps를 상속합니다. 즉, MsgOps와 MsgLaws는 같은 trait이라고 봐도 무방합니다. 별도의 trait으로 분리한 이유는 단지 기본 연산과 유도된 연산을 구분해 가독성을 높이기 위함입니다. 단, 스칼라는 서로 상속하는 구조를 금지하기 때문에, MsgLaws의 self를 MsgOps로 지정함으로써 이 문제를 해결했습니다.
이제 MsgOps에 선언된 기본 연산을 구현해야 합니다. 이를 다음과 같이 object Msg에 MsgOps를 상속한 뒤 object Msg에서 구현하겠습니다.
object Msg extends MsgOps {
...
def point[A](a: A): Msg[A] = apply(a)
def flatMap[A, B](msg: Msg[A], f: A => Msg[B]): Msg[B] =
msg match {
case MsgImpl(a) => f(a)
case _ => empty
}
def show[A](msg: Msg[A]): String =
msg match {
case MsgImpl(a) => a.toString
case _ => "empty"
}
}
MsgOps를 object Msg에서 구현한 이유는 두 가지입니다. 우선, Msg의 구현인 MsgImpl를 참조할 수 있는 범위가 private에 의해서 object Msg으로 제한돼있습니다. 따라서 MsgOps를 구현할 때 MsgImpl을 사용하려면 반드시 object Msg에서 구현해야 합니다. 두 번째로, object Msg에서 MsgOps를 구현하면, MsgOps의 연산을 사용할 때 Msg가 마치 네임스페이스나 패키지 이름처럼 보입니다. 즉, 연산을 Msg.show(msg)이나 Msg.show(msg1, msg2)처럼 호출할 수 있습니다.
편의를 위해 추가된 문법
앞서 Msg를 위한 연산 MsgOps를 object Msg에 구현함으로써 필요한 연산을 모두 호출할 수 있게 됐습니다. 하지만, 연산을 변수 앞에 적는 방식은 분명하지만 장황합니다. 따라서, 예를 들어 Msg.show(Msg.orElse(Msg.filter(msg1, _ == 0), msg2))같은 긴 연산을 짧게 적을 수 있는 방법이 필요합니다.
이를 위해 다음과 같은 문법적 편의(syntactic sugar)를 위한 클래스를 추가합니다.
trait MsgSyntax {
implicit class MsgSyntaxImpl[A](msg: Msg[A]) {
def flatMap[B](f: A => Msg[B]): Msg[B] = Msg.flatMap(msg, f)
def show: String = Msg.show(msg)
def map[B](f: A => B): Msg[B] = Msg.map(msg, f)
def filter(f: A => Boolean): Msg[A] = Msg.filter(msg, f)
def orElse[B >: A](msg2: Msg[B]): Msg[B] = Msg.orElse(msg, msg2)
}
}
이 MsgSyntax를 object Msg에 다음과 같이 추가합니다.
object Msg extends MsgOps {
...
object syntax extends MsgSyntax
}
그러면 import Msg.syntax._를 추가하는 것으로 Msg.show(Msg.orElse(Msg.filter(msg1, _ == 0), msg2))를 msg1.filter(_ == 0).orElse(msg2).show와 같이 가독성 높고 간략하게 표현할 수 있습니다.
다시 쓰여진 FizzBuzz 테스트
FizzBuzz 테스트를 풀 준비를 모두 마쳤습니다. 이제 다음과 같이 FizzBuzz 테스트를 해결할 수 있습니다.
import Msg.syntax._
val cd1: Int => Boolean = i => i % 3 == 0
val cd2: Int => Boolean = i => i % 5 == 0
val cd3: Int => Boolean = i => cd1(i) && cd2(i)
val tf1: Int => String = i => "Fizz"
val tf2: Int => String = i => "Buzz"
val tf3: Int => String = i => "FizzBuzz"
val inputs = (1 to 100).toList.map(raw => Msg(raw))
val outputs = inputs
.map(i =>
i.filter(cd3).map(tf3) orElse
i.filter(cd1).map(tf1) orElse
i.filter(cd2).map(tf2) orElse i)
.map(msg => msg.show)
println(outputs.mkString(", "))
이 해법은 1분만에 푼 해법에 비해 가독성이 높고, 재조합하기 쉽고, 테스트하기 쉽고, 새로운 요구조건이 추가되더라도 유연하게 대처할 수 있습니다. 예를 들어, 다음 조건이 추가된다면 어떨까요?
- 문자열 앞에 숫자를 추가하기 (예. “(15) FizzBuzz”)
- 입력된 숫자를 제곱한 뒤, 문자열로 변환하기
- 앞 숫자와의 곱을 문자열로 변환하기
- 입력으로 들어온 여러 종류의 숫자 중 정수만을 선별해 문자열로 변환하고 나머지는 무시하기
이 문제들 중 일부는 MsgLaws에 새로운 연산을 추가해야 하지만, 기본 연산이 정의된 MsgOps에 새로운 연산을 추가할 필요는 없습니다. 결국 앞서 정의된 기본 연산을 조합하는 것만으로 이 문제들을 해결할 수 있습니다. 즉, 단 세 개의 연산을 조합하는 것만으로 다양한 연산을 유도함으로써, 고려할 수 있는 수많은 문제들을 이 연산의 조합만으로 해결할 수 있게 되었습니다.
스칼라 클래스 형식의 요약
우리는 먼저 Data를 정의하고, Data를 다룰 수 있는 방법인 기본 연산 Ops와 유도된 연산 Laws를 정의했습니다. 그리고 편의를 위해 Syntax를 정의해 가독성을 높였습니다.
trait Data
trait Ops extends Laws {
...
}
trait Laws { self: Ops =>
...
}
trait Syntax {
...
}
object Data extends Ops {
...
object syntax extends Syntax
}
이 형식은 함수형으로 데이터를 다루는 수많은 문제에 일반적으로 적용될 수 있는 방법론입니다.
잘 짜여진 함수형 프로그램이 무엇일까요? 저는 이 형식의 관점에서, 프로그램이 요구하는 모든 연산의 기본 연산을 가능한 적은 갯수로 간결하게 정의하는 것이라고 보고 싶습니다.
이 포스팅에서 서술한 FizzBuzz 테스트의 전체 코드는 gist에서 조회하실 수 있습니다. 또, Scastie을 이용해 코드를 실행하거나 여러 가지로 변경해보실 수도 있습니다.
이 글을 재미있게 읽으셨다면, 이 포스팅에서 소개된 형식으로 작성된 통계 라이브러리인 Flip을 방문해 별을 눌러주세요!
더 읽을거리
빠르고 가벼운 통계 및 확률 라이브러리인 Flip의 대부분의 클래스가 이 포스팅에서 소개한 형식으로 작성되었습니다. 이 형식이 실용적으로 어떻게 적용되는지를 보고싶으시면 Flip 라이브러리의 확률 분포를 구현한 부분을 참고하세요.
simulacrum은 이 포스팅에서 성취하고자 하는 목적과 비슷한 목적을 가진 라이브러리입니다.
다음 몇 가지 포스팅은 위 라이브러리와 마찬가지로 이 포스팅과 비슷한 목적의 방법론을 보여줍니다.
다음 포스팅은 위에서 서술한 여러 방법론이 공통적으로 겪는 문제를 보여줍니다. 이 포스팅에서 소개한 형식은 아래에서 제시한 문제를 피해갈 수 있습니다.